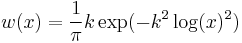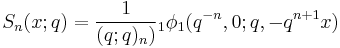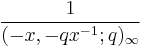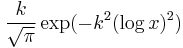Stieltjes–Wigert polynomials

Not to be confused with Stieltjes polynomial.

For the generalized Stieltjes–Wigert polynomials, see q-Laguerre polynomials.

In mathematics, Stieltjes–Wigert polynomials (named after T. J. Stieltjes and Carl Severin Wigert) are family of basic hypergeometric orthogonal polynomials in the basic Askey scheme, for the weight function

$w(x) = \frac{1}{\pi}k\exp(-k^2\log(x)^2)$

on the positive real line x > 0.

The moment problem for the Stieltjes–Wigert polynomials is indeterminate; in other words, there are many other measures giving the same family of orthogonal polynomials (see Krein's condition).

Roelof Koekoek, Peter A. Lesky, and René F. Swarttouw (2010, 14) give a detailed list of their properties.

1 Definition
2 Orthogonality
3 Recurrence and difference relations
4 Rodrigues formula
5 Generating function
6 Relation to other polynomials
7 References

Definition

The polynomials are given in terms of basic hypergeometric functions and the Pochhammer symbol by

$\displaystyle S_n(x;q) = \frac{1}{(q;q)_n)}{}_1\phi_1(q^{-n},0;q,-q^{n%2B1}x)$

(where q = e^–2k²).

Orthogonality

Since the moment problem for these polynomials is indeterminate there are many different weight functions on [0,∞] for which they are orthogonal. Two examples of such weight functions are

$\frac{1}{(-x,-qx^{-1};q)_\infty}$

and

$\frac{k}{\sqrt{\pi}}\exp(-k^2(\log x)^2)$

Recurrence and difference relations

Rodrigues formula

Generating function

Relation to other polynomials

References

Gasper, George; Rahman, Mizan (2004), Basic hypergeometric series, Encyclopedia of Mathematics and its Applications, 96 (2nd ed.), Cambridge University Press, doi:10.2277/0521833574, ISBN 978-0-521-83357-8, MR 2128719
Koekoek, Roelof; Lesky, Peter A.; Swarttouw, René F. (2010), Hypergeometric orthogonal polynomials and their q-analogues, Springer Monographs in Mathematics, Berlin, New York: Springer-Verlag, doi:10.1007/978-3-642-05014-5, ISBN 978-3-642-05013-8, MR 2656096
Koornwinder, Tom H.; Wong, Roderick S. C.; Koekoek, Roelof; Swarttouw, René F. (2010), Olver, Frank W. J.; Lozier, Daniel M.; Boisvert, Ronald F. et al., eds., NIST Handbook of Mathematical Functions, Cambridge University Press, ISBN 978-0521192255, MR 2723248, http://dlmf.nist.gov/18
Szegő, Gábor (1939), Orthogonal Polynomials, Colloquium Publications - American Mathematical Society, ISBN 978-0-8218-1023-1, MR 0372517
Stieltjes, T. -J. (1894), "Recherches sur les fractions continues" (in French), Ann. Fac. Sci. Toulouse VIII: 1–122, JFM 25.0326.01, MR 1344720, http://www.numdam.org/numdam-bin/item?id=AFST_1995_6_4_1_J1_0
Wigert, S. (1923), "Sur les polynomes orthogonaux et l'approximation des fonctions continues" (in French), Arkiv för matematik, astronomi och fysik 17: 1–15, JFM 49.0296.01